The Graceful Complexity of Nondeterministic Finite Automata
In the fascinating world of computer science, there lies a concept both elegantly simple and intriguingly complex: the Nondeterministic Finite Automaton (NFA). This concept, though it might sound intimidating at first, is a wondrous example of how the complexity of computation can be broken down into beautiful, understandable parts.
Imagine, if you will, a machine, not much unlike the computers we use every day. This machine has a set of rules, and it follows these rules to decide what to do next based on its current state and the input it receives. But here’s where the magic of NFA comes in: unlike the computers we're familiar with, which follow a single, deterministic path of computation, an NFA can explore multiple paths simultaneously. It's as if at every step, our machine clones itself, with each clone following a different potential path.
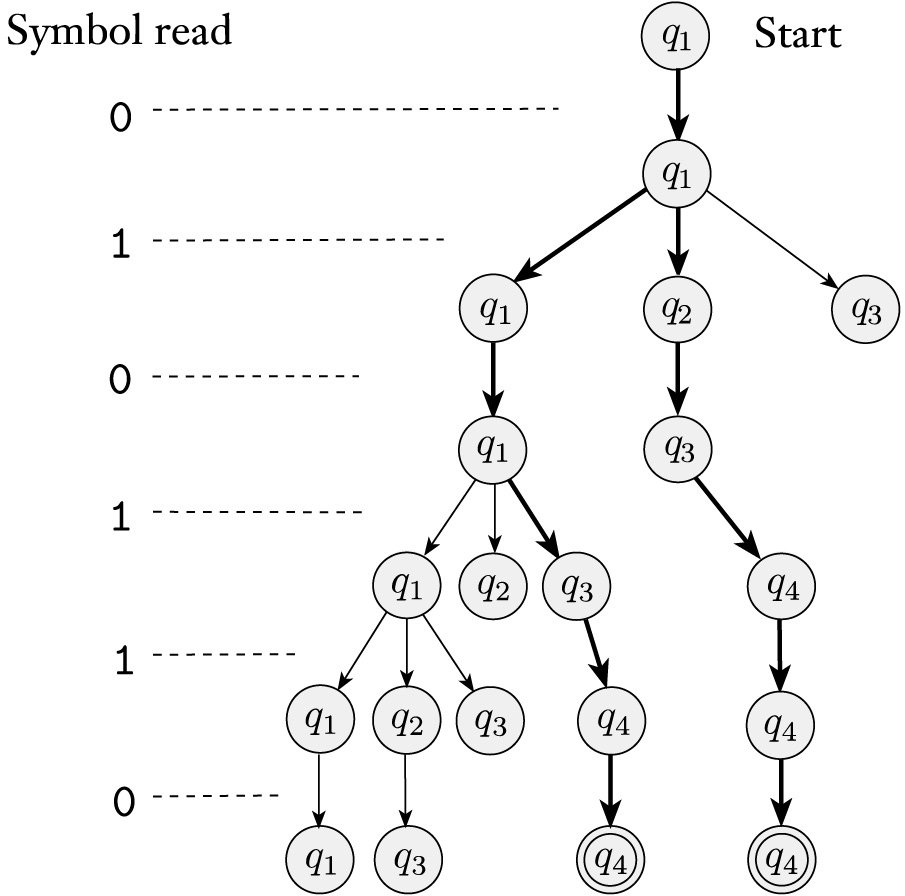
Take the following NFA as an example. What happened if it received 010110 as input?
©Introduction to Theory of Computation, Michael Sipser
Suppose I were at the state q1 and I read a 1. It encounters 2 options: either staying at q1 or moving forward to q2. Unlike the normal machine, NFA seems to self-duplicate into 2 threads. Like the following diagram shown:
©Introduction to Theory of Computation, Michael Sipser
Some states died out after the transition. For example, when the q3 receive a 0. It can’t accept it and therefore it died out.
This is the essence of nondeterminism. It's a kind of parallel computation, where multiple independent "processes" or "threads" run concurrently. Each thread represents a different possible outcome, exploring a different path through the computational landscape. It's like standing at a crossroads and being able to walk down every path at the same time to see where each leads.
Why is this beautiful? Because it speaks to a fundamental truth about our universe: the coexistence of multiple possibilities. Just as quantum particles exist in multiple states until observed, NFAs embody the concept of multiple realities in the computational realm. They remind us that at every moment, there are countless paths our lives could take, countless decisions and their myriad outcomes.
But it's not just a poetic notion. NFAs have practical applications, too. They are used in designing software, in understanding complex systems, and in theoretical computer science to explore the boundaries of what's computable.
In the end, the beauty of NFAs lies in their ability to make the complex simple, to take the tangled web of potential computation and lay it out in a way that we can see, understand, and marvel at. It's a reminder that sometimes, the most profound complexities can be understood through elegant simplicity.